Week 10 Assignment

Anova Testing & Linear Regression

Welcome to your FINAL module!

In order to streamline your work, I am inviting you to follow along for this week’s activity module with your OWN variables. You do not need to do the activity with my variables first. Just dive right in. My hope is that this will help you prepare for the final sections of your portfolio assignment.

Let’s begin by revisiting the ANOVA test

For this activity, I am imagining that my portfolio’s “umbrella hypothesis” is that “there’s something going on with race, education, and income.” Yes, your umbrella hypothesis can be that vague. We will get clearer hypotheses for our individual tests.

We will start by running some ANOVA (Analysis of Variance) tests, which means I need to get more specific about my hypothesis.

What should my hypothesis look like for a one-way ANOVA test?

Well, one-way ANOVA testing is a lot like t-testing, but it allows for more groups than 2! Which is good for me because the race variable in the GSS has 3 categories (white, black, other). If I were running a t-test, I’d have to recode that variable to a binary one.

One-way ANOVA tests allow us to compare groups within a categorical variable (can be any level but ideally you want only a few categories so if it’s ordinal or ratio you may want to re-code), but this variable (we’ll call it your “grouping” variable) should be a legible category of people. For example, the “sex” variable gives us legible categories of “male” and “female,” the “race” variable gives us legible categories of “white,” “black,” and “other.” Something like “income” would be a tricky grouping variable because “people who make $24,000 a year” isn’t a super legible category next to “people who make $24,500 a year” and “people who make $23,800 a year.” Make sense? So if you were using income as your grouping variable, you’d want to re-code it into legible categories like “low income” and “high income” homes. Make sense?

So pick your categorical variable first. (And evaluate whether you need to re-code it in any way). This will almost always be your “independent variable.”

Then select your interval-ratio variable. It should be interval-ratio level and continuous. (Again, evaluate whether it requires re-coding of some kind). This will almost always be your “dependent variable".”

For my one-way ANOVA test my categorical variable is:

“race”

For my one-way ANOVA test my interval-ratio variable is:

“conrinc” (a measure of income)

Now you have a ton of information here, but from your module last week, you should know that the within group and between group variation measurements (SS & MS), the df, the number of observations, are all just stepping stones to arrive at the “p-value” so you can direct your attention all the way over to the far right column where it says Prob>F. This is where your p-value (or your probability value) lives.

And it is just barely under .05, which is what we want! Because < .05 means less than 5%, so there is less than a 5% chance that our evaluation is incorrect, i.e. we can say with 95% confidence that we reject the null hypothesis that all the groups within the “race” variable are equal in income.

Put another way, there is a statistically significant difference in income between racial groups, in the American population.

Now try your own variables! Make sure to follow the directions step-by-step, and see if you can interpret your own p-value!

Two-Way ANOVA Testing

Now we will move into two-way ANOVA testing. Two-way tests allow us to incorporate additional grouping variables. So for this test, we have the opportunity to add on. I will use the same 2 variables from my one-way test, in order to demonstrate how you can abstract findings from the differences between the two outputs, and I recommend that you do the same.

So pick your interval-ratio variable first. (We are going to stick with “conrinc”)

Then select your categorical variable. We are going to stick with “race”

And now add additional categorical variables. I am going to add just one, for clarity. You may add one or more, but I’d recommend starting with one here. I have added “educ” which is a measure of years of education, because I am interested in how this “adds to the mix” between race and income.

Again, lots of information, but we will draw our attention to the far right column, to the “Prob>F” or “P-value” section of the output. What we see here is that the p-value for race has increased to .23 (above our .05 threshold of significance!). Which means that “race” has “dropped out” of our model when we incorporate education. Years of education remains at the <.05 level and is significant.

If we were interpreting just the above output alone…

we would say that there is a statistically significant difference in income between people of different education levels.

That is all we can report. In this model, when we account for education, we cannot reject the null hypothesis that the income means are statistically significantly different between racial groups, because the p-value on the race variable has fallen out of our desired range.

Note: We do not report that that difference does not exist. We just cannot report with confidence based on this model that it “doesn’t not exist.” Yup. Null hypothesis testing is a topsy turvy business.

If we were interpreting the above output alongside the first output…

You can see that without including “education” in the model (above left), there are observable, significant differences in income between racial groups… but when you include “education” in the model (above right), the significance of the race variable “falls away.” Looking at this we might start to wonder things like: “Oh maybe it’s not that race affects income directly… Maybe race affects “years of education” and “years of education” affects income!” Of course we don’t know the answer to this based on this model alone… but it clues us in to the fact that there is something going on, which we might address with other tests.

This “logic” is essential for techniques you will learn down the road if you continue in statistical work. Statisticians sometimes use “layering” techniques like this to see when and if the apparent influence of Variable A on Variable B “disappears” if you account for the influence of “Variable C.” This is how we might begin to consider variables that are mediating or confounding, which we discussed earlier in the semester (remember ice cream and crime?). More on this later.

Try the two-way anova test with your own variables! Add a new categorical variable, and interpret your output!

Linear Regression in Stata

We will cover some more detail on linear regression next week (there will not be an assignment, just a video to help you with your final portfolio work on linear regression) but this is an introduction. We will just learn how to run the regression in Stata, and I will talk about how to interpret it “in class.”

For the linear regression test, you need two continuous, interval-ratio level variables. Again, this might change your hypothesis a bit, or take you away from your umbrella hypothesis a little. That’s ok! Do the best you can.

Take a second to formulate your hypothesis.

For mine, I’ll be focusing on the “educ” variable, and the “hrs2” variable. But take a second to identify your variables, and your hypothesis. For linear regression, we will start with the simplest hypothesis there is: I hypothesize that there is a linear relationship between years of education and weekly work hours.

What’s yours?

Now the first thing we’re going to do is get back in touch with our old friend, the Pearson Correlation Coefficient. This is a helpful stepping stone on the way to interpreting linear regression (as you read for this week’s module).

As we were reminded in the lecture module, this signals to us an indirect, very mild relationship between the two variables, at a correlation coefficient of -0.22. We can think about this as a bit of information about our “slope” of sorts, remember? As education increases, work hours tend to decrease a little. But what we don’t know… is whether the relationship between educ and hrs2 is actually linear or not (i.e. can we actually model it with a y = mx + b equation?

*Note: I’m using hrs2 rather than hrs1, which only has 40 observations. You would never want to do this “in real life” but the linearity is a bit easier to see on hrs2 so pretend it has a larger number of observations

We will begin by creating a scatterplot of our data. Sometimes, as we discussed earlier this week, it helps us visualize how linear or nonlinear our variables are. (You’d also want to do some normality testing here, as I mentioned last week, but you don’t have to do this for the regression in your portfolio).

For me, it’s a bit difficult to see whether there’s any linearity here. (Think… “can I imagine a line of best fit here?”) I can “almost” see a slight trend downward, which makes sense, given the correlation coefficient.

What does yours look like for your variables? Does it appear to be linear? Take a second to interpret both the correlation coefficient and the scatterplot.

Now you’re ready to run the regression in Stata.

Running the Regression in Stata

The syntax is quite simple. The command is “reg” for regression. And you list what is theoretically your “dependent variable” first.

For me, the command is

reg hrs2 educ

Try your own!

Your output should look like the above.

Again, lots of information, but let’s focus in on what’s important. Check out the green highlighted areas below.

This is the first thing we are going to interpret. The p-value for our F-test: “Prob > F.” This is testing the null hypothesis that our model is useless and explains none of the variation in work hours. This is based on the R squared value below (yes this is the same R Squared from way back when we talked about correlation coefficients and shared variance! Welcome back, little guy!).

Unfortunately, our p-value is above .05. So my model is not statistically significant. In real life, we would move on and not interpret further, but because we are just learning, I am going to interpret the model as if it’s significant, and you should do the same for yours.

Take a second to interpret your own p-value. Is your Prob>F value above or below the .05 threshold? How would you interpret this?

Then check out the yellow highlights:

If you establish that the model is “good” using the green highlighted information, you would move on to interpret what’s highlighted in yellow. The yellow highlighted areas are the most important components of the output. But to understand them we have to re-orient to our “y=mx+b” formula.

y = mx + b

The highlighted coefficients above (in my case -1.11 on the “education” variable, and 47.7 on “_cons”) represent the “m” and the “b” of the line of best fit. But we need to make sure that these coefficients are statistically significant… so we will first check the column on the right for those p-values. You can see that the p-value on “cons” which is not a variable, just your constant or your 'y-intercept’ is significant. So that’s usable. But the p-value on your “x” variable, in my case “educ” is above .05. So this is not statistically significant in the model. In the real world, we would not incorporate this variable in our model as a result. But since we’re still learning. Let’s pretend that value is less than .05 and interpret it as if it’s significant.

So my linear line of best fit for this model would read:

y = (-1.11)x + 47.74

What’s your equation?

(Again, just pretend your coefficients are significant, but please not that it isn’t if they are not).

How would you interpret this? do you expect your “y” to increase or decrease as “x” increases? What’s your y-intercept? Interpret to the best of your ability using your own variables.

To see your line of best fit…

If you’d like to “see” your line of best fit, mapped onto your scatterplot, this is another way to visualize the information above. To do this, use the following command (with your own variables). It is a 2-step command.

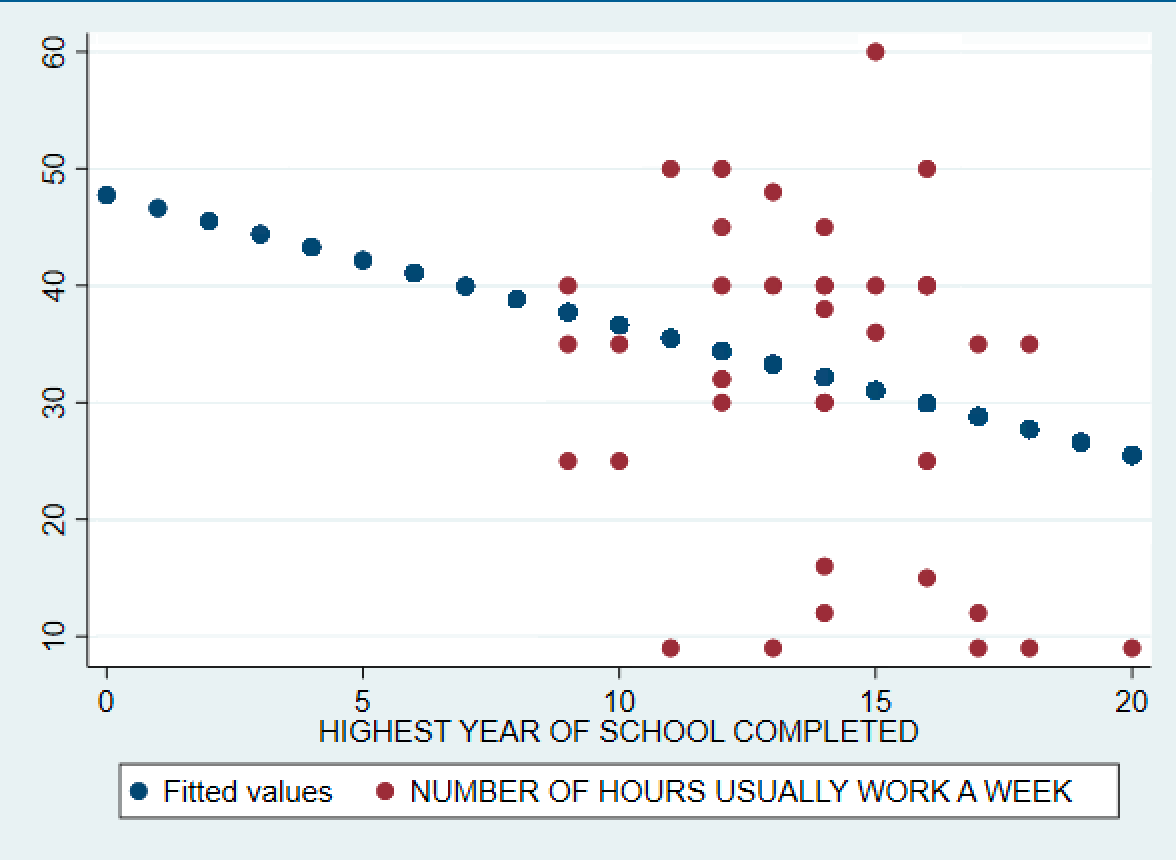
predict yhat

scatter yhat hrs2 educ

Your output should look like this. Predictably… our line of best fit doesn’t look much like our data at all… and this is because our model isn’t very good! Try with your own variables. What does your line of best fit look like? How would you interpret this?

Alternatively… (recommended for your portfolio)

Now I’m going to offer a sleeker way of doing a best fit line using a confidence interval. I would actually recommend that you try this one for the portfolio, as I think it’s clearer. This time I’ll use the variables:

agekdbrn: age at which first child was born

educ: number of years of education

I’m going to use this syntax:

graph twoway (lfitci agekdbrn educ)(scatter agekdbrn educ)

This is asking Stata to provide a two-way graphic, of a “llfitci” which is a line of best fit with a confidence interval, on top of a scatterplot of agekdbrn and educ.

It provides this output:

The green dots are your scatter. Your navy blue line is your best fit line. And the grey boundary is your 95% confidence interval around the best fit line.

You can think about this the same way you’d watch a hurricane tracker, where the predicted path is mapped (line of best fit) and the “cone of possible directions” is included as well. That “cone of possibility” (confidence interval) generally tells you that we’re “pretty sure the hurricane will hit somewhere in here between Florida and Virginia,” but that you “predict” (line of best fit) that it will hit Miami. Make sense?